Nevatim Strike: Accuracy Digestif

Iran’s recent missile strikes on Nevatim Air Force base only achieved limited damage, but it did give us a lot of data to play with to see precisely how accurate their missiles are under real world conditions. I’ve already crunched the numbers and they’re not particularly impressive. Iranian missiles likely have a CEP of around 800-900 meters, potentially as good as 500 meters if you make a series of extremely favorable assumptions for Iran. None of these numbers allow Iran to conduct economic counterforce targeting. Let me walk you through how I got there, partly because it’s great fun, and partly because it should cause you to think twice about talking about the CEPs of missiles.

How do we measure the accuracy of ballistic missiles? Generally accuracy measurements are presented in terms of the circular error probability, or CEP. It’s important to properly understand what this metric means. You may read that a missile has an accuracy of say, 30 meters. Most of the people who read this metric will come away with the idea that said missile will land within 30 meters of the target 100 percent of the time. This is not how probabilities work. Instead, a CEP measures the radius around the target the missile will land 50% of the time. If you’re targeting a small target with a 30 CEP missile, most of your shots are probably going to miss if you require a direct hit to destroy the target.

Misunderstanding this metric is part of the reason why people seem to have a pretty grossly inflated view of the effectiveness of most missiles. There are, of course, exceptions – missiles with advanced optical seekers are going to have higher accuracy than others. But most missiles that rely mainly on GNSS and INS for guidance have serious limitations, and generally advertised CEPs will not match the CEP the missile achieves in real world conditions. The CEP measurements you read about in the manufacture brochures are generally not based on coherent testing data, and instead are based on the theoretical performance of the missile in perfect conditions.

For example: Pershing 2 had an advertised accuracy of 30 meters. How many flight tests did the Army conduct with the Pershing 2? 23, and five of those were before the Army added Pershing 2’s incredibly advanced radar-guided warhead (of the early 5 tests, the Pershing 2 only achieved the desired accuracy 1 time). Of the remaining 18 tests (which was originally supposed to be 28 tests) the missile exploded prematurely 4 times, and an additional 5 reported partial or complete failures of various onboard subsystems. An additional test was aborted when the missile failed to ignite. It also worth noting that ALL of the 18 later tests were partial tests. At no point before its deployment did the Army successfully test the Pershing 2 to its full range against a land-based target and actually come anywhere close to a 30-meter CEP.

If you include all of this in a real-world calculation of the missile’s accuracy and its mission success rate, you will come away with a missile that will not achieve a measured 30-meter CEP and with a mission success rate of around 50% depending on how you count some of the tests. Does this mean that the Pershing 2 is a bad missile? God no. Pershing 2 is one of my favorite missiles, and it achieved its purpose: scare the shit out of the Soviets.

So going into this discussion of the measured CEPs of Iranian missiles, I want you to keep those things in mind. A system’s listed CEP is an approximation of accuracy assuming everything works under clean, testing conditions. This isn’t to try and claim that American missiles are as inaccurate as Iranian missiles or anything like that – more to simply make the point that you should be skeptical of any system’s stated CEP without real world data.

Now, let’s dig into it. The simplest way we could calculate the CEP of Iran’s missile forces based on the data we have is simply by counting up all the points and then calculating the average longitude and latitude values and treating the resulting point as the intended target. I’ve done this below simply because it’s a good visual of a CEP in theory. Each red dot on the map below is an impact point. We calculate the average XY point, which is marked by the white target. Once we have that, we can collect the radial distance from this central point of each impact point, and then find at what distance 50% of the points are included. This will give us a CEP. This is a bad way of doing it and will give you a CEP that is much larger than the actual performance. It’s included only to help explain the concept, and to give you an example of what you shouldn’t be doing.

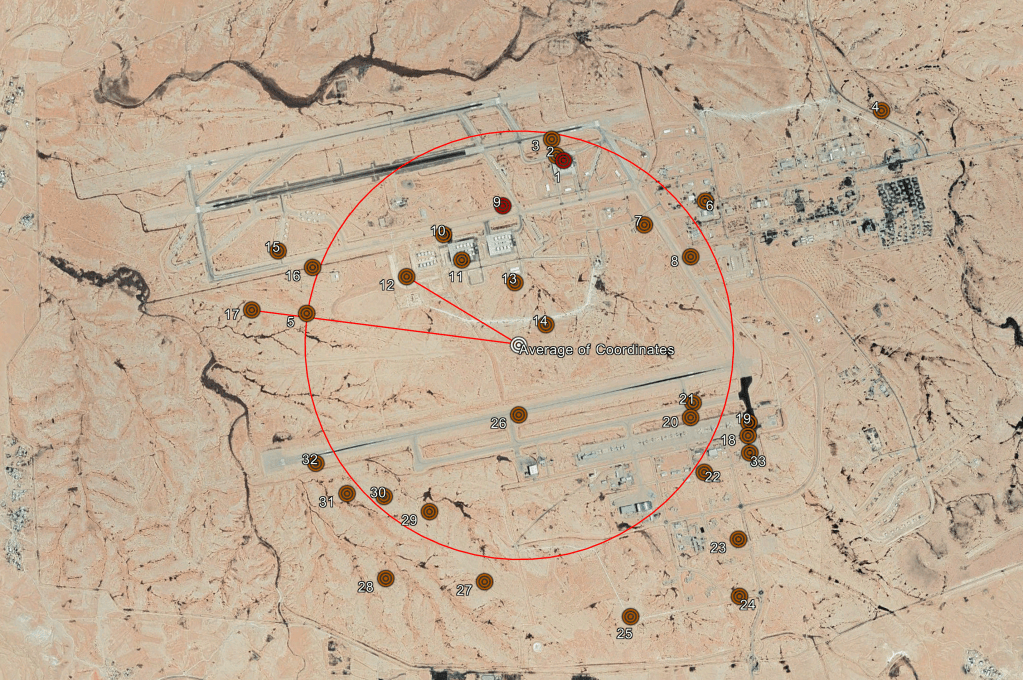
There are two major problems with attempting to calculate a CEP this way. The first is that long-range missile impact distributions aren’t circles. A CEP assumes that the distribution of impact points is a circular distribution. However, missiles are carrying a tremendous amount of momentum in one direction, which means a missile has a much greater chance of either undershooting or overshooting the target (referred to as a down-range miss) than hitting far to the side of a target (referred to as a cross-range miss).

Look at the distribution of impact points again. At first glance the distribution of points may appear circular, but note that there is a break between the impact points on the northern area of the base and the southern area of the base. Likely what actually occurred is that Iran targeted two areas, one on the above runway, and one on the below runway. That means we are not actually dealing with a circle at all, and instead dealing with two long ellipses, seen below. This checks out when you factor in Iranian launch positions, by the way – the angle of the ellipses matches the direction of several Iranian missile bases that we know Iran launched from, like Imam Ali Missile Base outside Khorramabad.

The second problem is that we don’t know the aim point(s). We cannot simply assume that the aim point is in the middle of each ellipse, and without that assumption, CEP calculations get really wonky really fast. I tried plugging in the data to either ellipse into several CEP calculations used to determine GPS accuracy, and once you start moving the intended target away from the middle of the ellipse, the CEP it calculates begins to grow exponentially as the probability that the points would be placed in the distribution they are is so unlikely if you are assuming the distribution should be circular.

So what do we need to do? Instead of relying on radial distance, we need to calculate the X-axis miss distance and the Y-axis miss distance for each target point individually to compensate for the difference between the two. We don’t actually know the target point, but the clustering can give us some clues. Iran likely targeted the hangars on one end of the south runway (where, I should mention, the Israeli presidential plane was intermittently stored following some domestic political controversies in Israel regarding its use) and the F-35 shelters along the north runway. For reference, south runway hangers are near impact points 18, 19, 20, 21, 22, and 33, and the F-35 structures are near impact points 1, 2, 3, 9, 10, 11, and 12. Below I have added my assumed target points for both the northern and southern ellipses. This is, again, basically a best guess based on the distribution of impact points and what sort of high value targets Iran would actually want to hit.

The target selection is the most arguable part of this as we obviously don’t know what precise area the Iranians targeted. We’ll discuss running this with different target points and changing other variables later, as you can improve the CEP somewhat. But I believe that the target points are reasonable due to where the high level targets at Nevatim.
Now, for each ellipse, we need to calculate the distance from the target point along both the X and the Y axis for each impact point. Below is an example of the information we need.

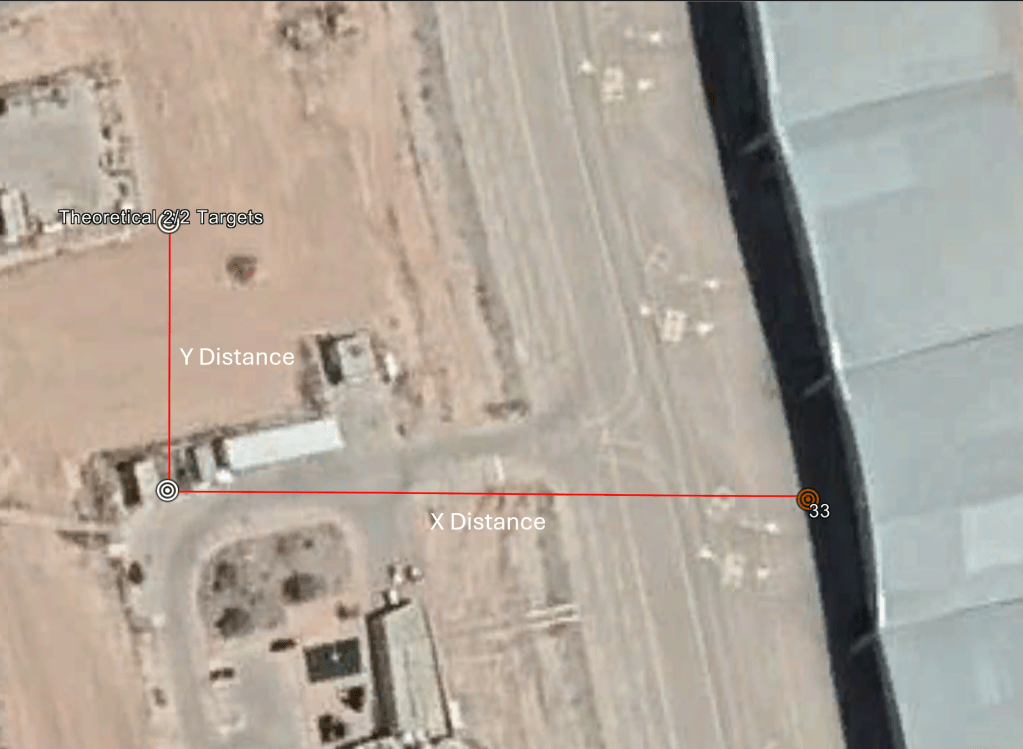
Once we’ve calculated all that for each target, we should have a table of data that allows us to start to calculate something like an approximate CEP of Iranian missiles, and one that compensates for the fact that the distributions along the X axis and the Y axis are going to be very different. Thankfully some much MUCH smarter people have written out some helpful formulas that I can use. Take a look at this document that my former colleague Sam Lair pointed out to me. The document gives us several ways of approximating the CEP from non-circular information, and I am using this formula:

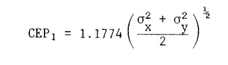
Let’s plug in the data! Taking the standard deviation of the X and Y values for each ellipse and then taking the average of the two, we get an approximate CEP for Iranian missile accuracy of…908 meters. I don’t think I need to spell out how bad that is. Here’s a visualization of that CEP approximation below. I should drive home the point that this is an approximation, and that as missiles don’t have circular distributions of impacts, no CEP measurement is truly going to cleanly match the data.

Again, this measurement assumes my assessment of what was likely targeted is correct. You can improve this somewhat if you change the target points to be closer to the center of each ellipse (say, near target points 11 and 26). If you run that calculation you get a CEP of around 500-600 meters, but again, the distribution of target points makes that target point selection unlikely, especially in the bottom target set.

One thing we have to account for is the theoretical performance of Israeli missile defense. Perhaps the CEP is not as high as it would be in real world conditions as many of the missiles that would have hit important targets were intercepted by Israeli missile defenses. This is incredibly unlikely for several reasons, the main one among them being that Israel’s primary interceptor operates in the mid-course, when it’s very difficult to tell whether any particular missile is going to hit the target. The sort of missiles Iran launched has the capability to maneuver after the mid-course as they are entering the atmosphere, which means Israel doesn’t have a way to accurately determine the impact points of such missiles during the time period where it would be intercepting them (generally, I acknowledge that David’s Sling appears to have managed 1 or 2 intercepts). But let’s head off this potential counterargument by doing some thought exercises.

Iran launched 180 ballistic missiles at three target sets at Israel. Let’s imagine this was split evenly (60/60/60) and we are missing 27 impact points at Nevatim. We have a list of probable impacts, so let’s actually say we’re missing 20. Let’s assume that 10 of those missiles failed to get to Israel for whatever reason (a 17% failure rate, which is very reasonable for ballistic missiles!), so we’re missing 10 impacts.

Now let’s assume, simply for the sake of the argument, that all of those 10 missiles would have hit something important. Let’s plot them here as hypothetical impacts (the points in white).

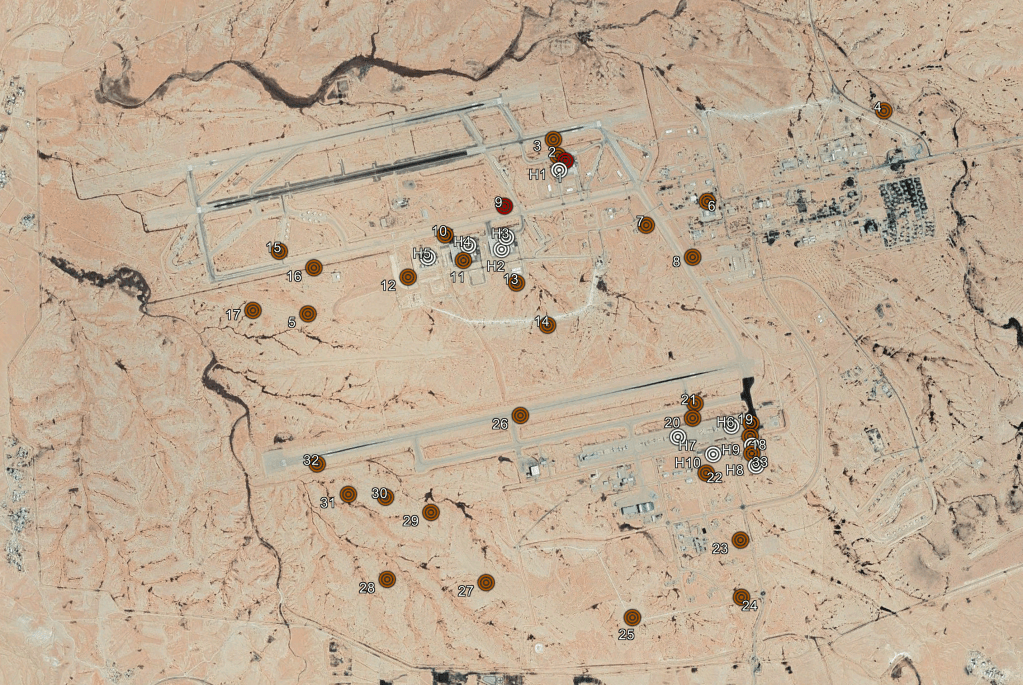
I crunched the numbers again using these calculations. Does this improve the accuracy calculations? Yes, but not by much. We’ve improved the accuracy from 908.163 meters to 863.363 meters. That’s still not great! Adding more missiles on target would only further reduce the range by small amounts. Why? Because of the number of overshoots. If we were to simply exclude those (points 5, 15, 16, 17, 27, 28, 29, 30, 31, and 32) from the dataset, the CEP would become better, but still not great. I crunched the numbers a bunch of times playing with removing overshoots and assuming less likely target points, and in no simulation does the CEP of these missiles break 500 meters. I think a real CEP of around 800-900 meters is the likeliest scenario here given the data. Even under the most favorable set of assumptions for Iran, Iranian ballistic missiles clearly do not have precision accuracy.

Now for part two. We now have some data on the accuracy of Iranian missiles. What we’re going to do now is calculate the chance that a single Iranian missile can destroy a counterforce target. This metric is known as the single shot probability of kill (SSPK) and is calculated with the following formula:

SSPK=1-0.5^(RL/CEP)^2

Where RL is the “lethal radius” of the missile. It’s basically how close a missile has to land in relation to the center of the target to destroy it. This can get complicated with some targets as you need to know the blast pressure wave generated by the missile warhead and how much pressure would be required to destroy the target.  Lets consider the SSPK of a single Iranian missile against a single, isolated F-35 hardened aircraft shelter (HAS). We don’t need to worry about blast pressure with a HAS in these circumstances because we can safely assume that only a direct hit can destroy or heavily damage a HAS if you’re using a 650 kg warhead. If your HAS does not survive a miss with a 650 kg conventional warhead, then the HAS has failed its purpose.

The radius of a HAS target at Nevatim is 10 meters, so let’s treat that as the lethal radius for a direct hit and plug that into the equation along with the CEP to calculate the SSPK of a single Iranian missile against a specific HAS. Not a set of HASs or the HAS area, one, specific, 20 by 20 meter target.

1-0.5^(10/908)^2 = 0.0000840689

So a 0.008% chance of scoring a hit on that target.

Just for the sake of argument, let’s put in 600 meters, which is still a terrible CEP, but is in line with an incredibly generous depiction of Iranian missile performance.

1-0.5^(10/500)^2 = 0.00027722043. That’s 0.03%!

Again, this is the chance one missile will score a hit against a single specific HAS. We see better performance at Nevatim, but that’s because Nevatim has many hardened aircraft shelters distributed over a wide area. Once you account for the chance that at least one missile will strike at least one target, your hit chances get much better – although I don’t see much mileage in doing a Monte Carlo simulation here as the result would be specific to Nevatim. By changing the assumptions, we can see Iranian missiles likely have a CEP between about 700-1000 meters. The difference between those two numbers doesn’t mean much for the rate of success at either SSPK is unworkable for counterforce. The bottom line here is that, even under a set of assumptions that are most favorable to Iranian missiles, you cannot get results from the data that suggest these missiles are capable of economic counterforce targeting.

Israeli conventional and nuclear forces aren’t in existential danger of Iranian missile strikes unless Iran dramatically increases the scale of attacks against target complexes. Iran may be able to destroy major Israeli ground army bases and major administrative complexes if they are sufficiently tightly packed, but this will likely not sufficiently degrade Israel’s strike capabilities against Iran. This doesn’t mean Iran won’t be able to do significant damage and kill lots of people. Their long-range missiles are simply too inaccurate to match the sort of precision strikes we saw on October 25th. This suggests – as I think we’ve already seen recently – that there are hard limits on the deterrence benefits of Iranian missile forces. If you can only credibly threaten cities, then you can’t threaten targets that you could hit at lower rungs of the escalation ladder. This means you aren’t really able to effectively deter low level tit-for-tat conflicts like the one Israel and Iran are currently embroiled in. The result is that Iran and Israel may be stuck in a small stability-instability paradox, as Israel is clearly not willing to use nuclear weapons to respond to or deter Iranian missile strikes, and Iranian missile strikes are only really going to be effective at targets you attack at very high levels of escalation and thus are not capable at deterring Israel. This suggests that Israel and Iran trading missiles is going to be a long running problem going forward. Iran getting the bomb is really only going to make this problem worse, as Iran having a dedicated nuclear force would likely lower the number of missiles they need to keep in reserve for escalation, which means more conventional missiles to throw at Israel.

This could change if Iran produces missiles capable of striking counterforce targets. Once Iran proves it can destroy a large number of Israeli F-35s with conventional missiles, their missile forces will begin to pose a serious threat to Israel at low levels of escalation. But until Iran makes those improvements, we’re stuck here.